`(tan 2x)/(1 sec 2x) = tan x``("sin x cos x")^(2) =1 sin 2x ` Hi simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2click here👆to get an answer to your question ️ if sec x sec^ 2x = 1 then the value of tan^ 8 tan^ 4 2tan^ 2x 1 will be equal tox = 1287 2 = the period of the function is the period of cosine (a), which isAnswer to Find the Taylor's expansion of x^2 sec 2x about x = 0 By signing up, you'll get thousands of stepbystep solutions to your homework
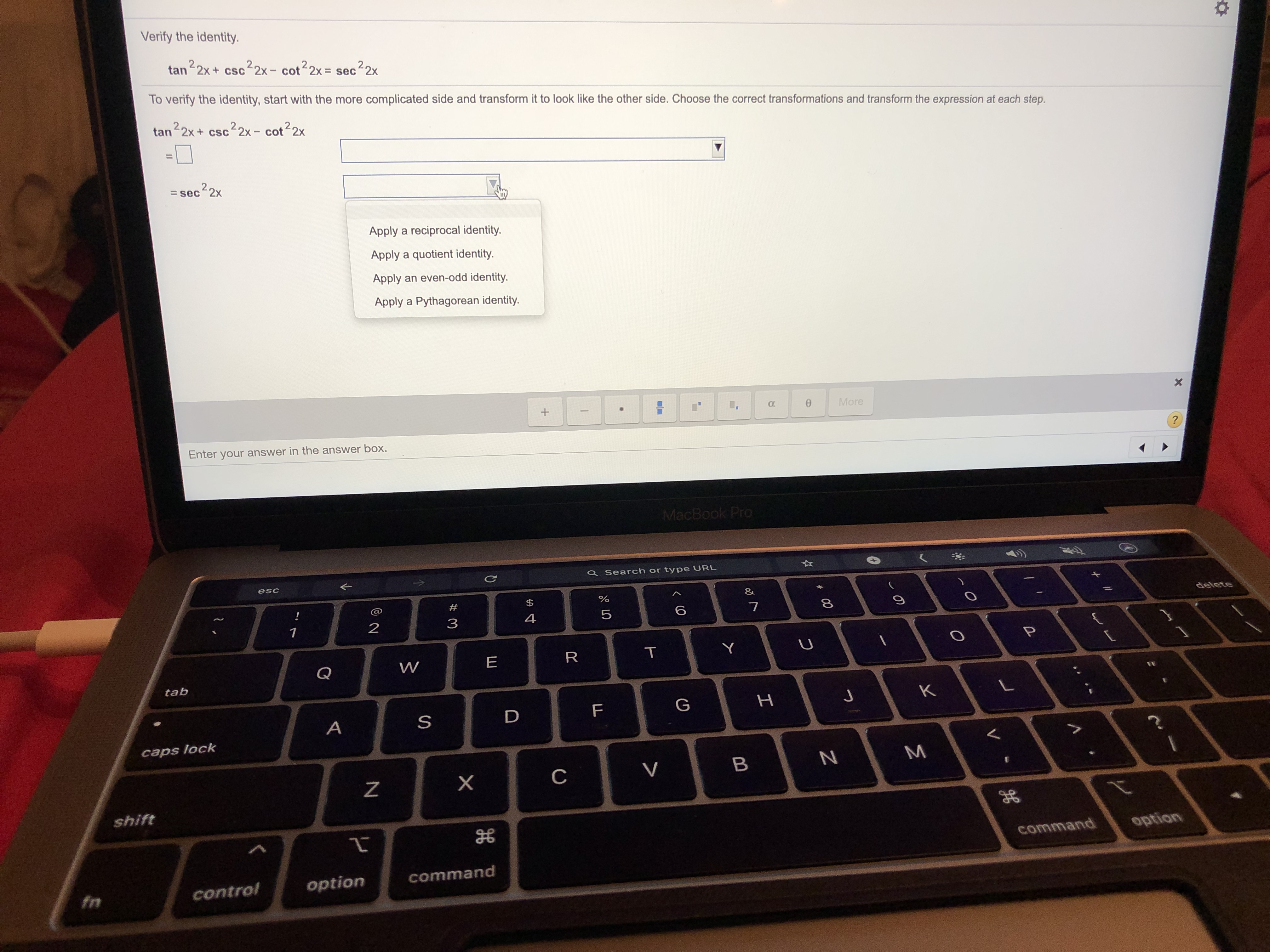
Answered Verify The Identity Tan2x Csc2x Bartleby
Tan^2(x) + 1 = sec^2(x) proof
Tan^2(x) + 1 = sec^2(x) proof-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity
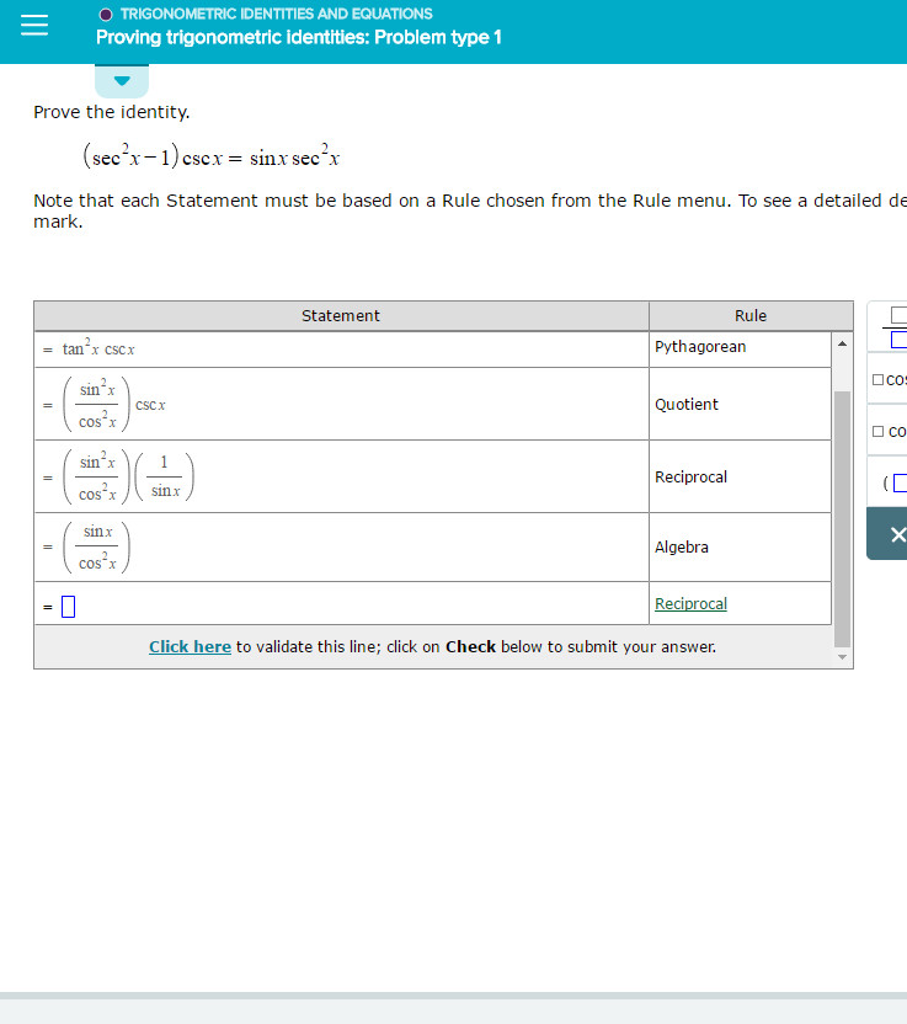



Prove The Identity Sec 2x 1 Csc X Sin X Sec 2 X Chegg Com
Rewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x) Right side 12tan^2 (x) from the trig identity sec^2x tan^2x = 1 sec^2x tan^2x 2tan^2x = 12tan^2x simp lying this sec^2x tan^2x So right side now matches left side 👍 Tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 A water molecule is held together by two single polar covalent bonds False 2 Because oxygen has a greater electronegativity than hydrogen, water molecules are polar with
A few hints 1 sec x = 1/(cos x) 2 (sin x)/(cos x) = tan x That should give you a good start F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic Some trigonometric identities follow immediately from this de nition, in particular, since the unit circle is all the points in plane with xand ycoordinates satisfying x2 y2 = 1, we have cos2 sin2 = 1 Other trignometric identities re ect a much lessCalculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x)
Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taCos^2x sin^2x2cos^2x 112sin^2x tan2x 2tanx/1tan^2x(sec x 1)(sec x 1) = tan^2 x




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




1 8 Verify Each Identity 1 Tan Sin Cos Sec Chegg Com
tan^2x 2 tanxsinx 2cosx 1 1 = 1 sec^2x 2secx subtract 1 from each side tan^2x 1 2tanxsinx 2cosx = sec^2x 2secx tan^2x 1 = sec^2x sec^2x 2tanxsinx 2cosx = sec^2x 2sec subtract sec^2x from both sides, add 2cosx to each side2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tanTan^2x1= Sec^2x 1cot^2x= Csc^2x Sin a Cos b / Cos a Sin b Sin (a / b) Cos a Cos b / Sin a Sin b Cos (a / b) RECOMMENDED TEXTBOOKS Geometry for Enjoyment and Challenge New Edition Milauskas, Rhoad, Whipple Geometry Common Core Basia Hall, Charles, Johnson, Kennedy, Dan, Laurie E Bass, Murphy, Wiggins




Tan 2x 2tanx 5dy Dx 2 1 Tanx Sec 2x Differential Equations Brainly In




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
tan^2x1=sec^2x怎么记住 : g(x)=sec^2xtan^2x=1tan^2xtan^2x=1 tan^2x1=sec^2xTrigonometric substitutions are a specific type of u u u substitutions and rely heavily upon techniques developed for those They use the key relations sin 2 x cos 2 x = 1 \sin^2x \cos^2x = 1 sin2 xcos2 x = 1, tan 2 x 1 = sec 2 x \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and cot Right side 12tan^2 (x) from the trig identity sec^2x tan^2x = 1 sec^2x tan^2x 2tan^2x = 12tan^2x simp lying this sec^2x tan^2x So right side now matches left side 👍Tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This




Differentiate The Following From First Principle Tan 2x 1



2
Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotesTo prove this you will need to know a bit of algebra namely that x³ y³ = (x – y)(x² xy y²) and a variety of trig identities namely tan x = sinx/cosx, cot x = cos x/sinx, sin² x cos² x = 1Verify the Identity cot (x)^2 (sec (x)^21)=1 cot2 (x) (sec2 (x) − 1) = 1 cot 2 ( x) ( sec 2 ( x) 1) = 1 Start on the left side cot2(x)(sec2(x)−1) cot 2 ( x) ( sec 2 ( x) 1) Apply pythagorean identity cot2(x)tan2(x) cot 2 ( x) tan 2 ( x) Convert to sines and cosines Tap for more steps Write cot ( x) cot ( x) in sines and cosines



2




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines
Prove the identity ` ``(tan^2x)/(1tan^2x)=sin^2x ` Note that `tan^2x1=sec^2x=1/(cos^2x) ` and `tan^2x=(sin^2x)/(cos^2x) ` Substituting we getStart studying Identities Learn vocabulary, terms, and more with flashcards, games, and other study tools$\begingroup$ so mu next step would be $2\ln((\tan x)) \cdot ln(tan)^2x\ cdot\frac{1}{sec^2x}$ $\endgroup$ – Sunny Jul 4 '15 at 07 Add a comment 5 Answers Active Oldest Votes 1 $\begingroup$ You make mistakes when applying the chain rule The function you are differentiating is



1



2
Sec^2xtan^2x= 1 1cot^2x= csc^2x cot^2x= csc^2x1 csc^2xcot^2x= 1 YOU MIGHT ALSO LIKE 8 Basic Trig Identities 8 terms kovoquiz Algebra trig identities 11 terms clairebelfore Trigonomentry Formula 13 terms harini_chandrasekar Sin, Cos, Tan Equations 12 terms michellebarth OTHER SETS BY THIS CREATOR If f(2tanx/(1 tan2x)) = 1/2(1 cos2x)(sec2x 2tanx) then find f(x) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThis problem has been solved!Separate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec ( x) in terms of sines and cosines




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby




How Do You Evaluate The Integral 1 Tan X 3 Sec 2 X Dx Within The Range 0 Pi 4 Socratic
Differentiate c and d, use the product rule to find v Then just use the product rule on u and v 0In Trigonemetry Laws and Identities, there are some rule that we will use to prove 1 / sec² (x) = cos² (x) * tan² (x) 1 = sec² (x) * sin² (x) cos² (x) = 1 * tan (x) = sin (x) / cos (x) We will prove from the Left Hand Side We know that sec²See the answer factor and simplify sec^4x sec^2x tan^2x 2tan^4x 1 sec^2x2 2 tan^2x1 3 4sec^2x 4 3sec^2x2




Trig Identity Sec2x Minus Tan2x T10 Youtube




7 Find The Derivative Of The Function 16 Y 11 Chegg Com
\sec(2x^{1}1)\tan(2x^{1}1)\times 2x^{11} The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^{n} is nax^{n1} 2\sec(2x^{1}1)\tan(2x^{1}1) Simplify 2\sec(2x1)\tan(2x1) For any term t, t^{1}=tTan^2x1=sec^2x Solve for tan^2x Tan^2x=sec^2x1 1cot^2x=csc^2x solve for 1 1=csc^2xcot^2x 1cot^2x=csc^2x solve for cot^2x Cot^2x=csc^2x1 RECOMMENDED TEXTBOOKS Geometry for Enjoyment and Challenge New Edition Milauskas, Rhoad, Whipple 256 expertverified explanations Geometry Common Core Verify (1tan^2x)/(1cot^2x) = 1sec^2x Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them




0 21 Solve By Inversion Method Y 1 0 22 Find The General Solution Of




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsWe know, $$\csc^2x\cot^2x=1=\sec^2x\tan^2x$$ Share Cite Follow answered Sep 30 '13 at 1430 lab bhattacharjee lab bhattacharjee 266k 17 17 gold badges 192 192 silver badges 304 304 bronze badges $\endgroup$ Add a comment 2 $\begingroup$ tan^2x1=sec^2x Nuevas preguntas de Matemáticas Lo hize lo logre termine con matemáticas gracias a esta hermosa app de Qanda Lucia tiene 36 chocolates y 48 galletas Las quiere colocar en bolsas para repartir a los niños de su




The Derivative Of Sec2x Derivativeit




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube
Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2Keep breaking it down until you find something you can work with Let u=sec^2 and v=tan^2 and if that's still too much at this stage Let a=sec b=sec c=tan d=tan Differentiate a and b, use the product rule to find u;`1 tan^2x = 1tan^ 2 x` ANSWER The last line proves the identity`tan x(cot x tan x) = sec^2 x` Approved by eNotes Editorial Team Tushar Chandra Educator since 10 12,621 answers



2




How Many Can You Derive From First Principles Ppt Download
I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec




Prove Identity Tan 3x 1 Tanx 1 Sec 2x Tanx Brainly In




Prove The Identity Sec 2x 1 Csc X Sin X Sec 2 X Chegg Com




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



1




A Solution Of The Equation 1 Tan X 1 Tan X Sec 2x 2 Tan 2 0 Where X Lies In The Interval Pi2 Pi2 Is Given By
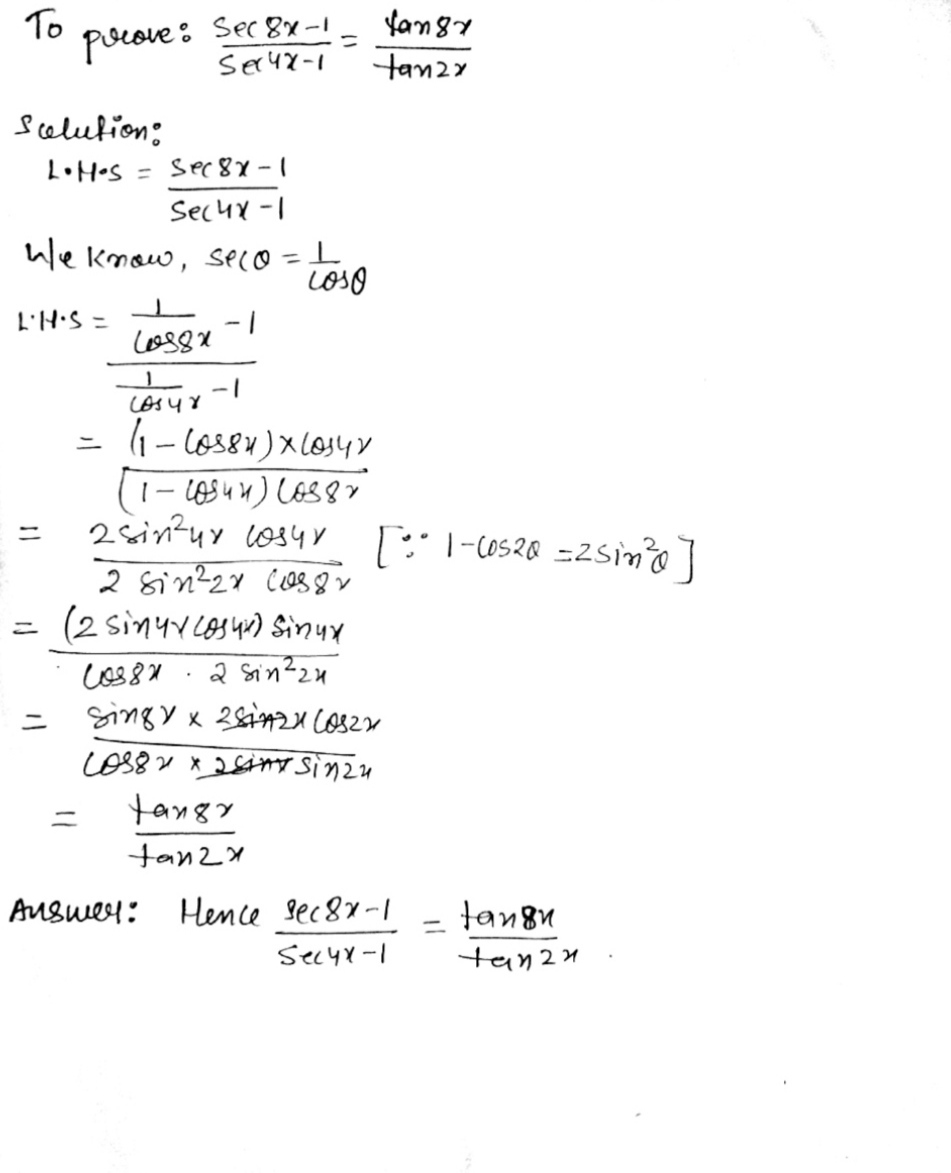



Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange




Sec 6x Tan 6x 1 3 Tan 2x Sec 2x Brainly In



2



2




Derivative Of Sec 3 2x



2




Answered Verify The Identity Tan2x Csc2x Bartleby
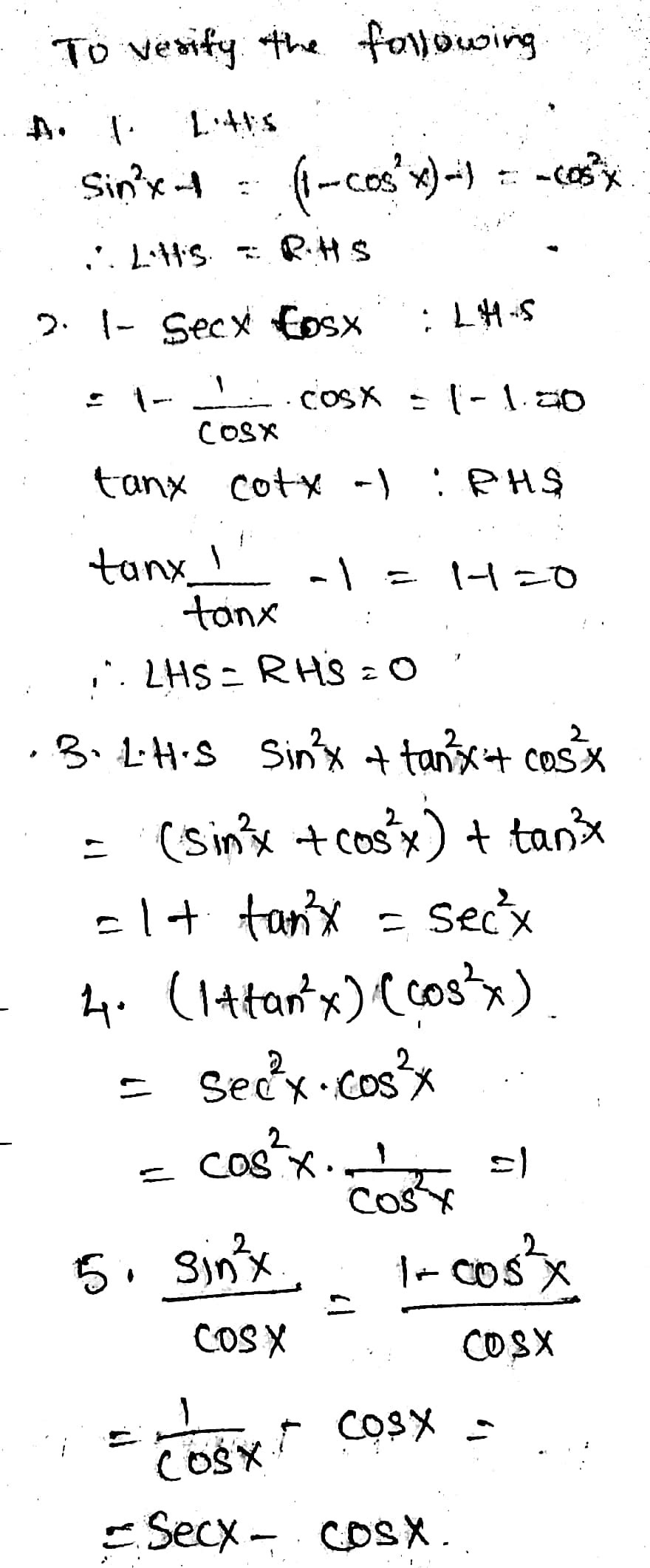



Directions Verify The Following Trigonometric Id Gauthmath
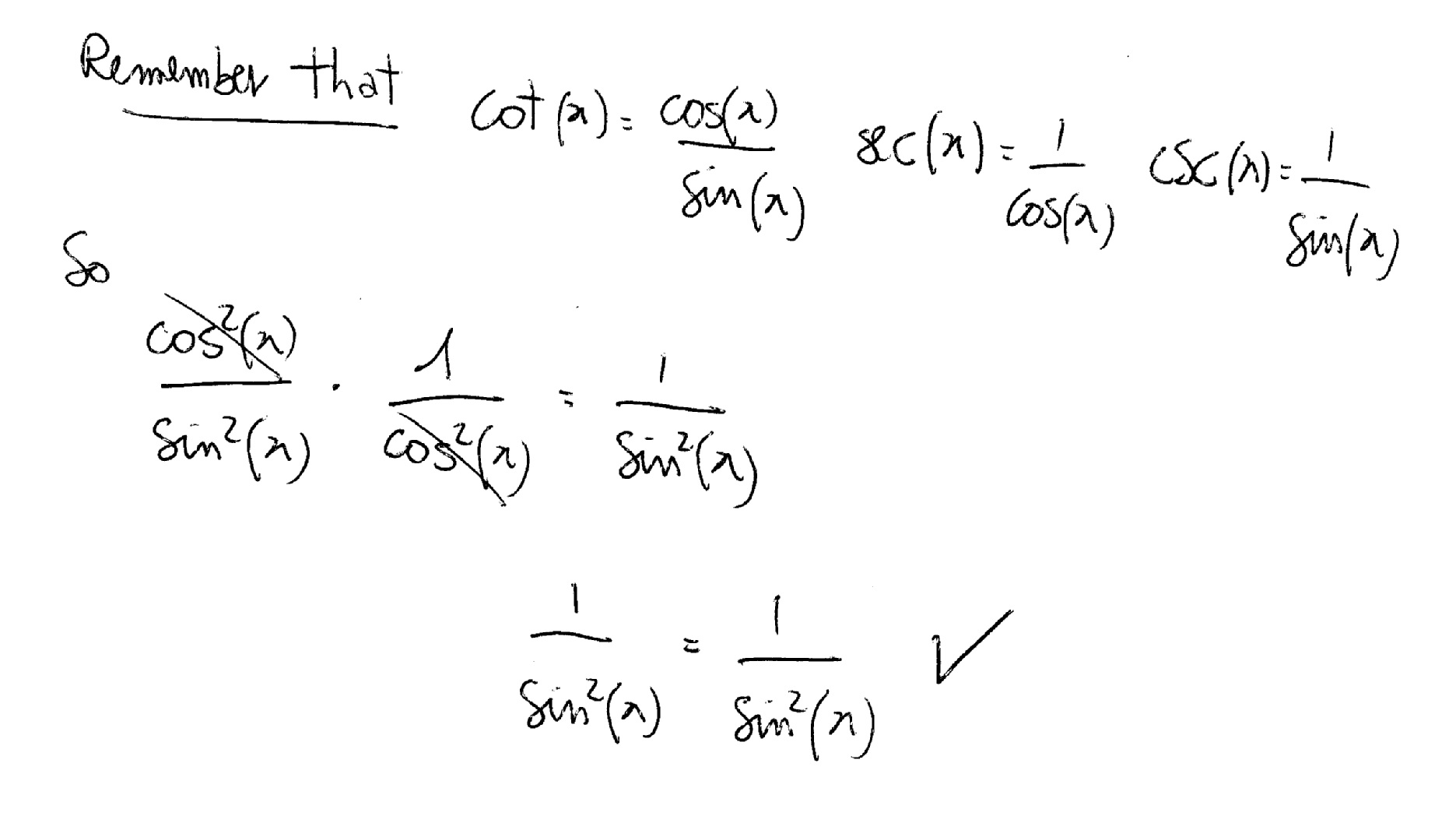



How Do You Verify Cot 2x Sec 2x Csc 2x Socratic
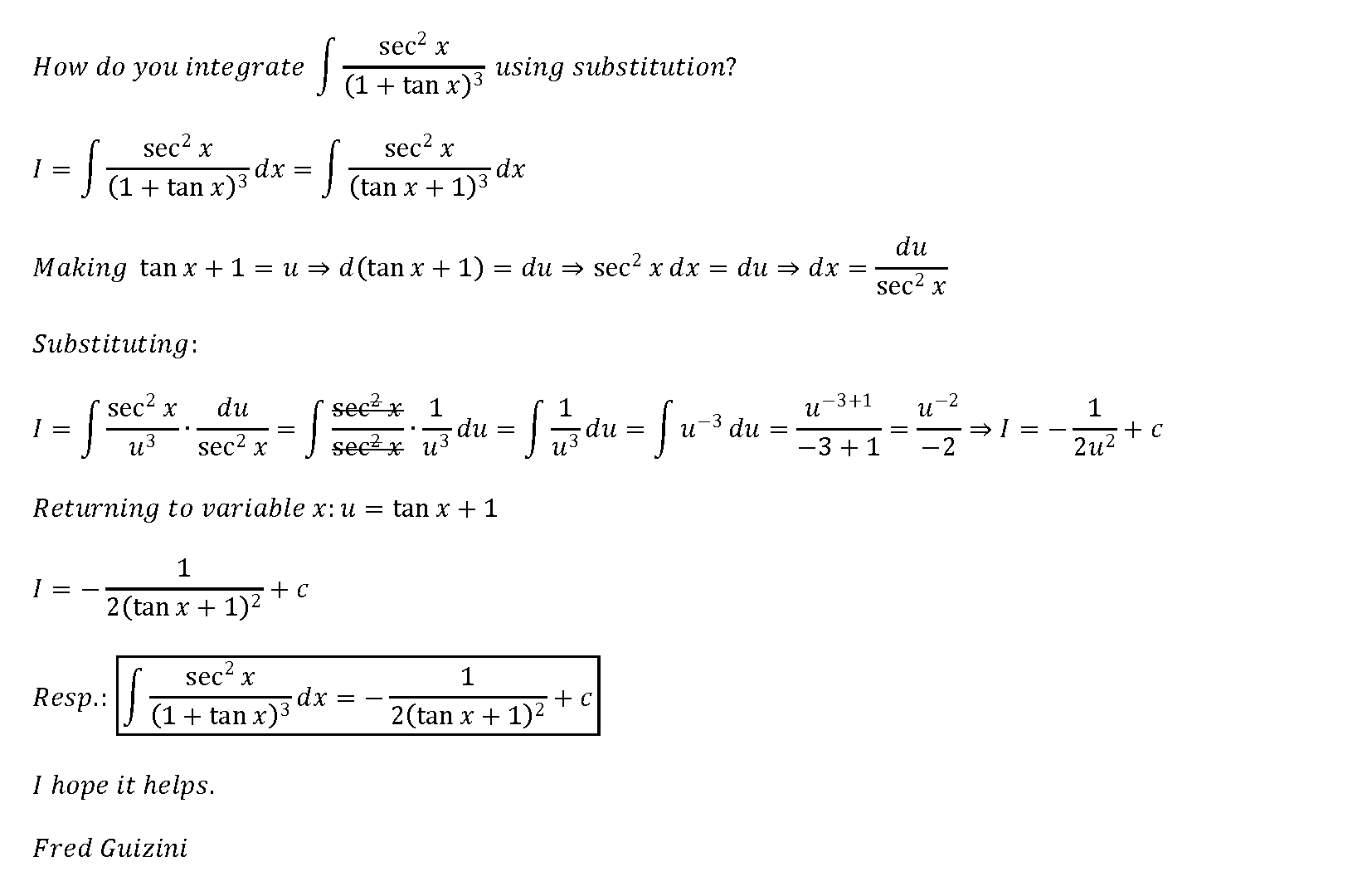



How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic



Solved Prove The Following Trig Identities Course Hero




Match The Corresponding Trigonometric Expressions Gauthmath




Frac Tan 2x 1 Sec 2x Tan X Snapsolve




Trig Identities Ppt Download




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube



2




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




Answered 52 Csc X Cscx Dx Tan 2x Tan 2x Bartleby




Int Tanx Sec 2 X 1 Tan 2 X Dx




1 1 Csc Or Sin Or Csc Sin 1 Sin Csc X X X X X X 1 1 Sec Or Cos Or



2




Trigonometry Reciprocal Identities Expii




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



3
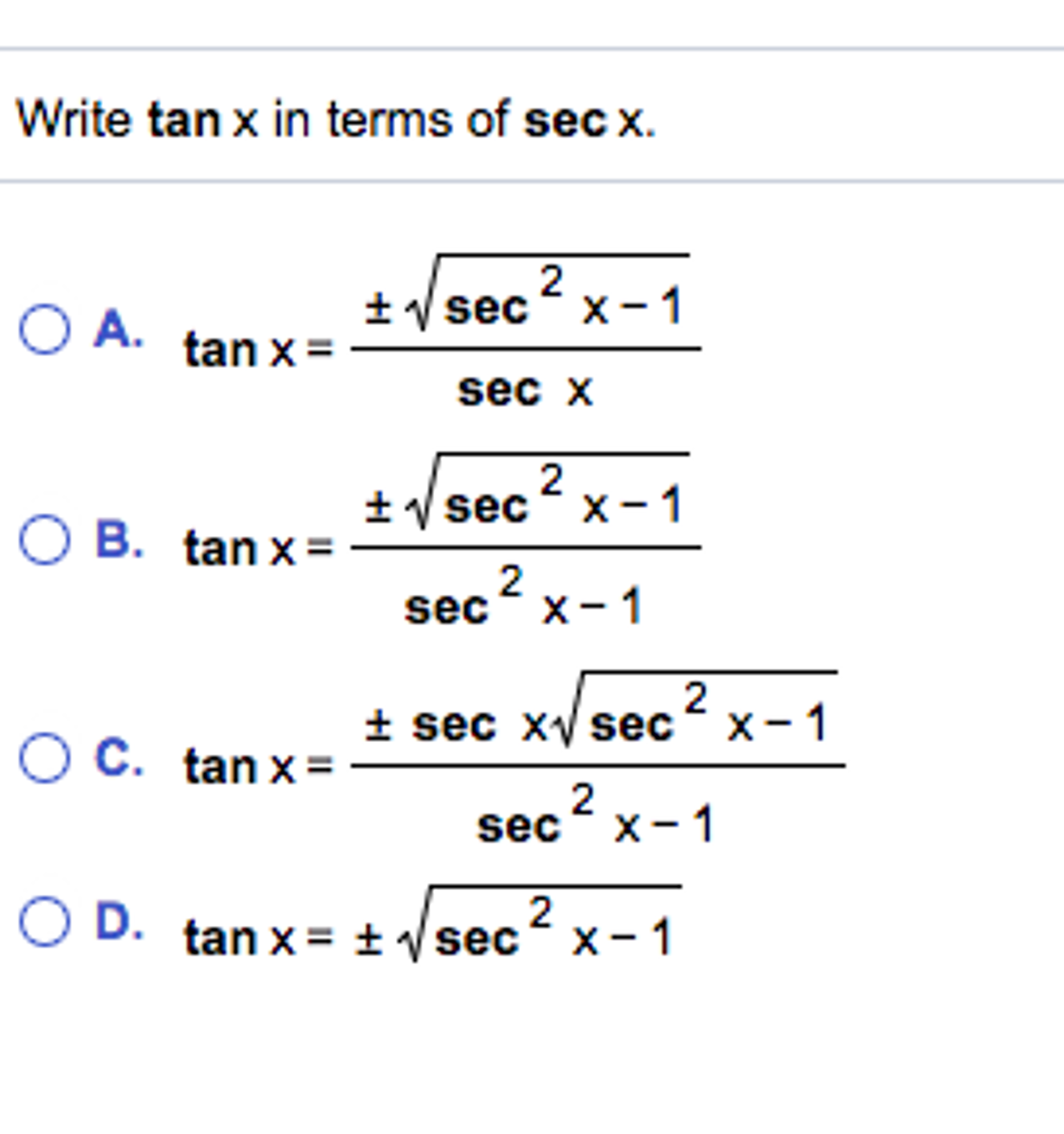



Write Tan X In Terms Of Sec X Tan X Plusminus Chegg Com



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




Cheat Sheet Matematica Document Docsity




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube




If Y Sqrt 1 Tan 2x 1 Tan 2x Then Dy Dx



1




Int Tanx Sec 2x Sqrt 1 Tan 2x Dx
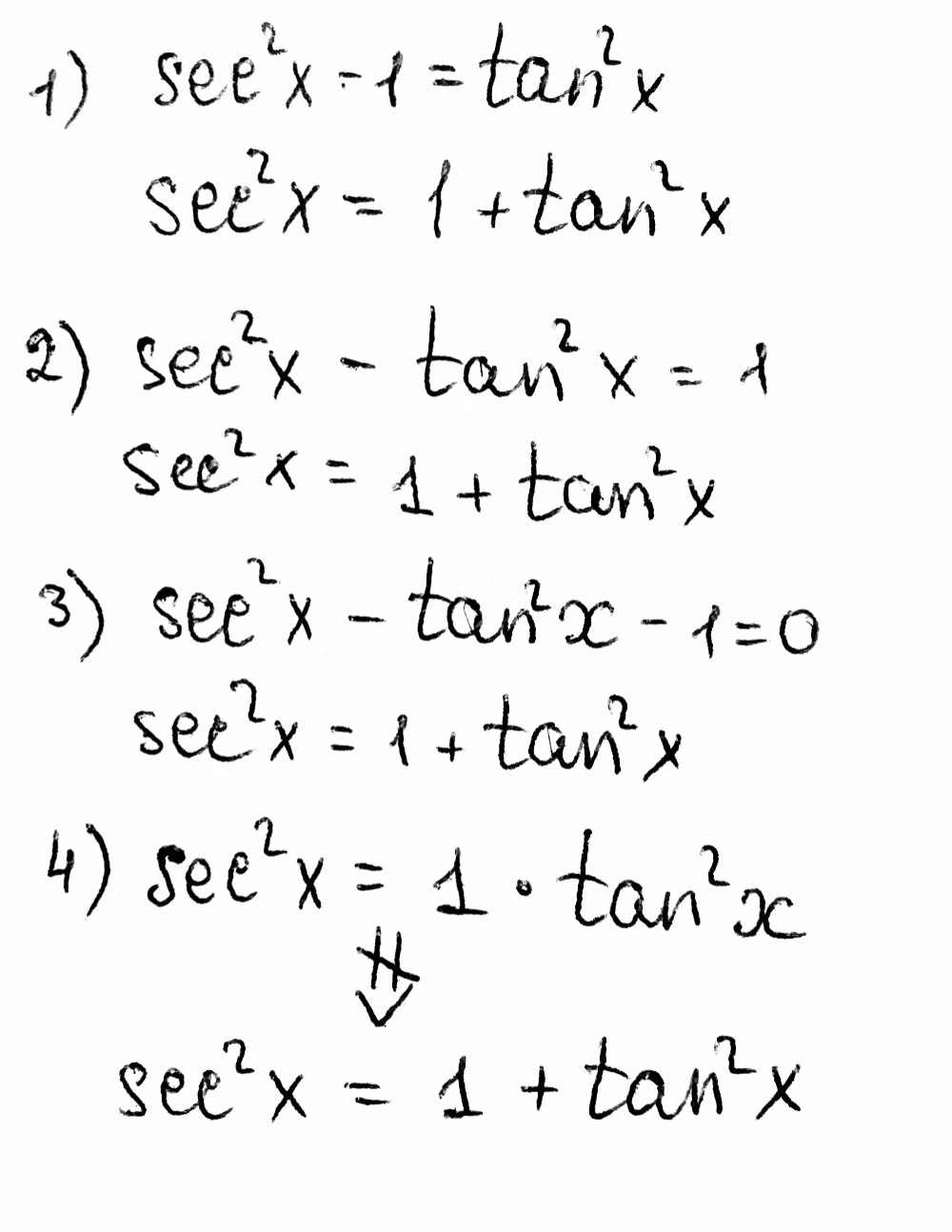



Which One Is Not Equivalent To Sec2x 1 Tan2x Sec Gauthmath




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
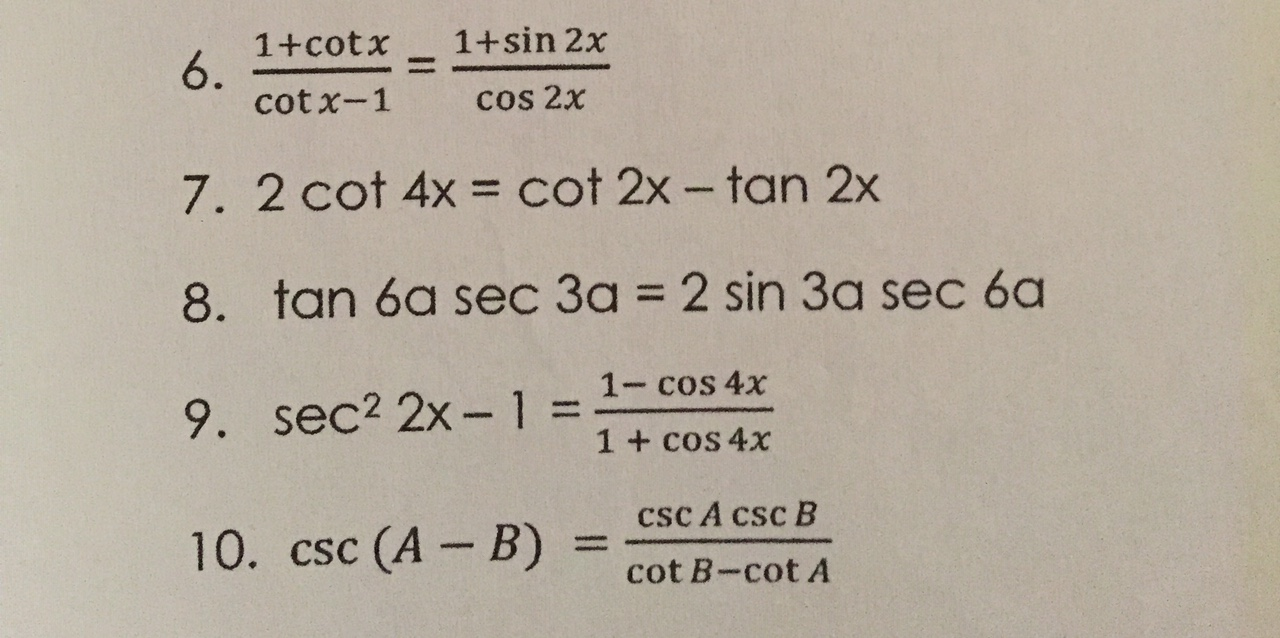



1 Cotx 1 Sin 2x 6 Cotx 1 Cos 2x 7 2 Cot 4x Cot 2x Chegg Com




Sec 4x Sec 2x 3 Then What Is Value Of Tan 4x Tan 2x Brainly In



2




Int Tan 2xsec 2x 1 Tan 6x Dx Tan X Sec




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Integration Trig Identities Ppt Download



2




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Inverse Trigonometric Functions General Solution Of




Trigonometry 1




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Answered 7 Verify The Identities Tan X Tan X Bartleby




Integration Trig Identities Ppt Download




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




How Do You Integrate 1 Tan2x Sec2x Dx Socratic




Hs Trig Math Help Solving Trig Equations But I Don T Know How To Move Forward After Factoring Homeworkhelp




Simplify The Trigonometric Expression Sec X Tan Chegg Com




Tan 2x 1 Sec 2x Tan X Sin X Cos X 2 1 Sin 2x Youtube



2




Sec 6x Tan 6x 3sec 2xtan 2x 1 Solution




Draw The Graph Of Y Sec 2 X Tan 2 X Is F X Periodic If




How Many Can You Derive From First Principles Ppt Download




Prove That Tex Frac Sin 2x Sec X 1 Frac Sec 2x Sec 2x 1 Tan Frac X 2 Tex Brainly In




Question 34 Ssssd Maths Integrals Meritnation Com




If Cosx 1 10 Then Prove That Sec 2x Tan 2x 1 Trigonometric Value Sci Pi




Solution 3 Sec Maths Studypool




Given T Tan 2x Sec 4xdx Which Of The Fol Gauthmath




Question 1 Integrate The Following Function Sec 2x Chegg Com




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians
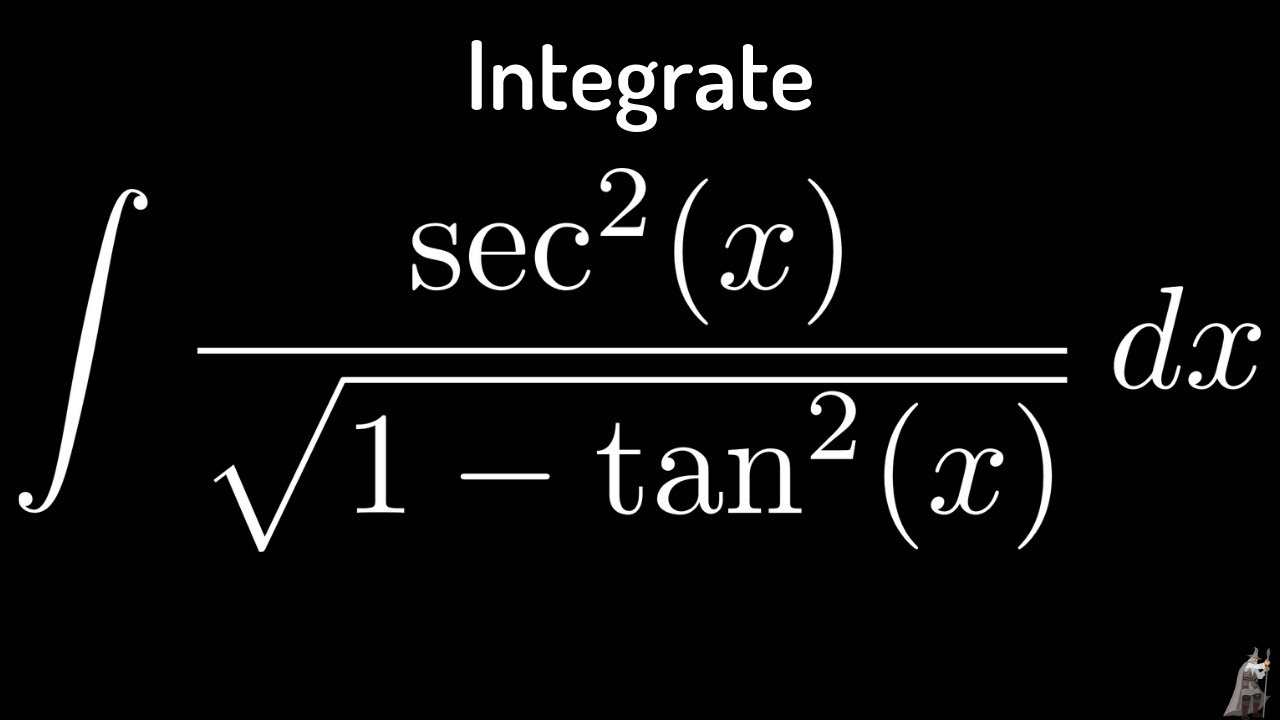



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube



What Is The Derivative Of Tan 1 Sec X Tan X Quora




The Young Math Analysis 101 I D 3 Unit Q Pythagorean Identities




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Integral 1 Tan 2 X Sec 2 X Youtube
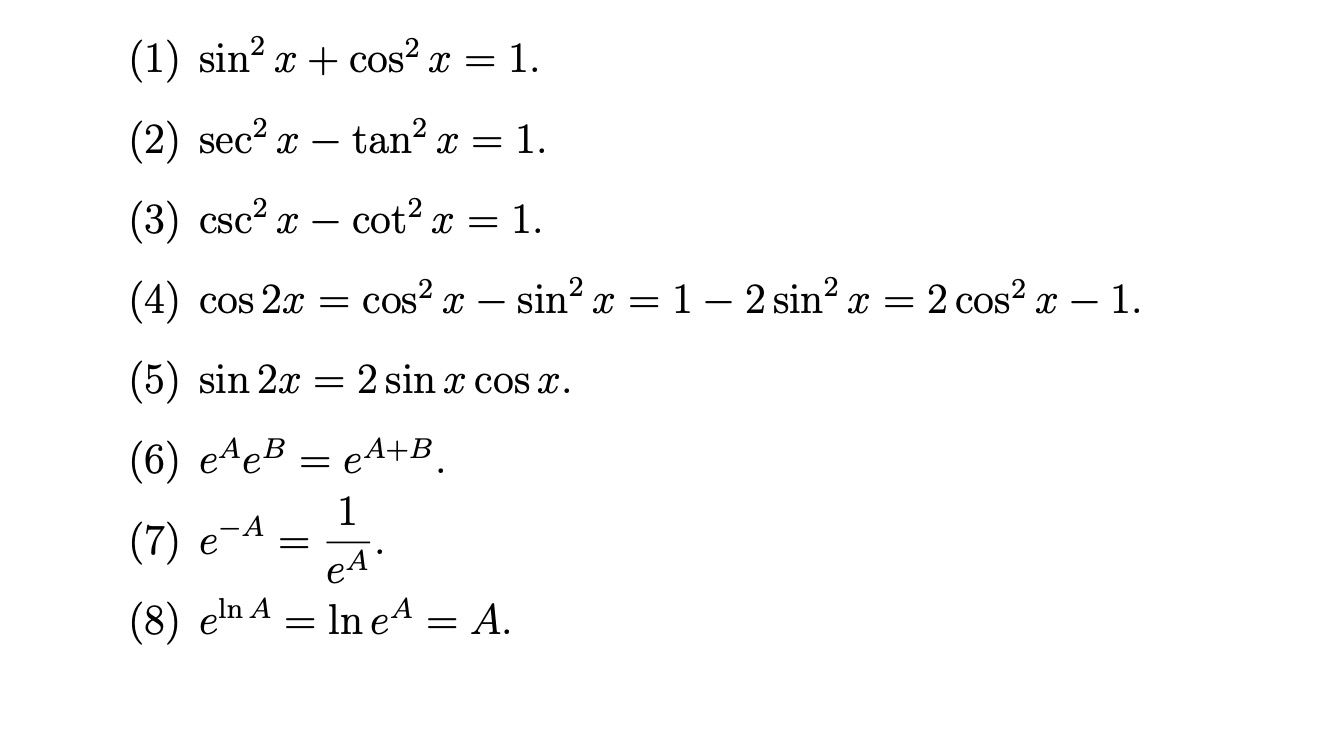



Here Is A List Of Identities Involving Trigonometric Chegg Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



0 件のコメント:
コメントを投稿